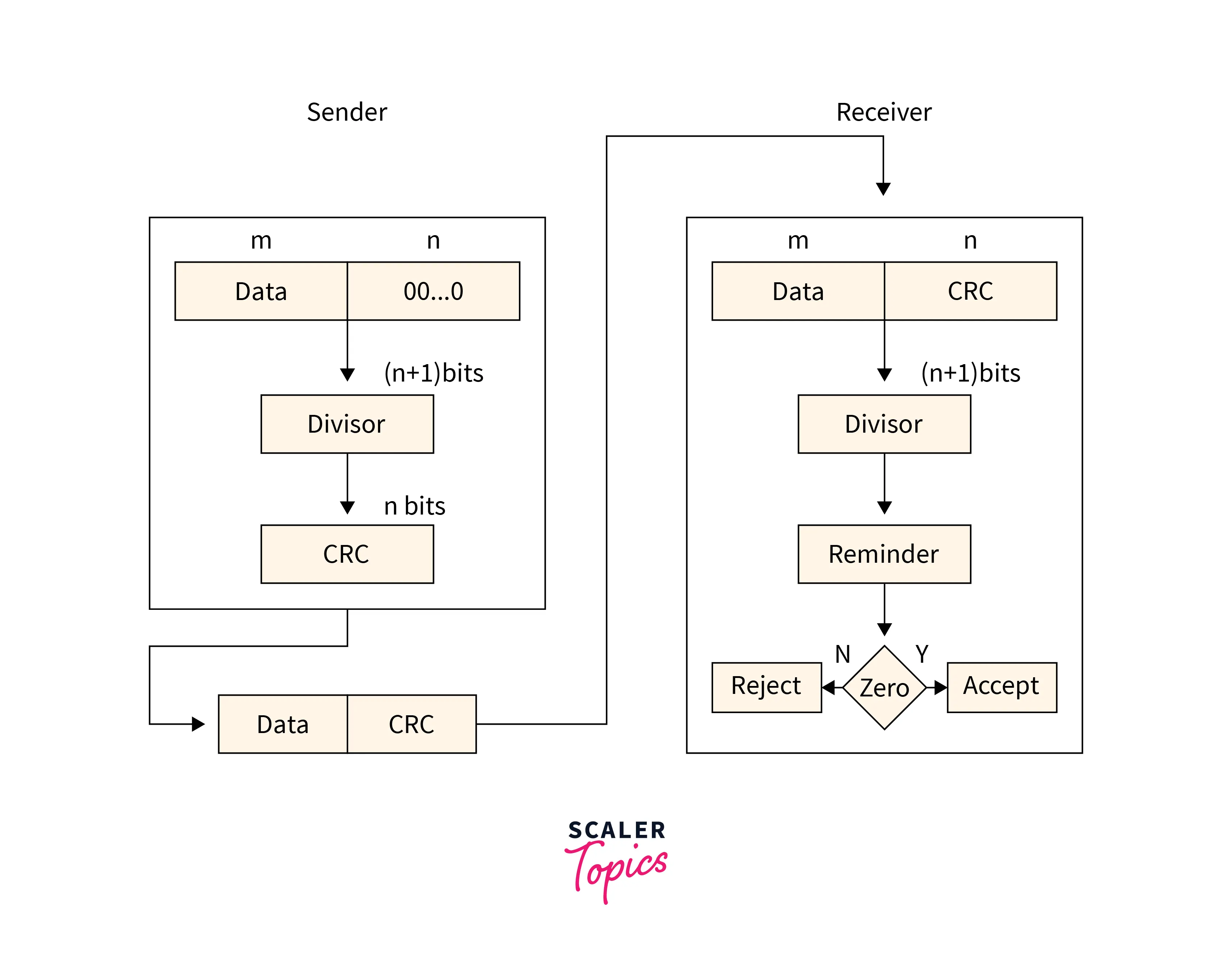
Cyclic Redundancy Checksum (CRC)

Cyclic Redundancy Check (CRC) is an error detection method that uses polynomial arithmetic to check data integrity. Here’s a summary of how CRC works and an example calculation.

CRC Process

1. Representation: Treat the data packet as a polynomial.
2. Division: Divide this polynomial by a generating polynomial using polynomial arithmetic.
3. Remainder: Append the remainder of this division to the end of the message.
4. Verification: The receiver performs the same division with the appended message. If the remainder is zero, the message is error-free.

CRC Flow

Example Calculation with Polynomial $(x^3+x+1)$

Step-by-Step Example

Data Polynomial: $(1101)$ (binary representation, which corresponds to $(x^3+x^2+x^0)$)

Generator Polynomial: $(x^3+x+1)$ (binary representation $(1011)$)

1. Append Zeros: Append 3 zeros to the data polynomial, where 3 is the degree of the generator polynomial.

   • Extended Data Polynomial: $(1101)$ becomes $(1101000)$

2. Division: Perform polynomial division of $(1101000)$ by $(1011)$.

   • Binary Division:

     1101000 ÷ 1011
     

   • Perform Division:

       1011 | 1101000
             1011
             ----
             01100
              1011
             ----
              0101
               1011
             ----
                0100
     

   • Remainder: The result of the division is $(100)$.

3. Append Remainder: The remainder $(100)$ is appended to the original data polynomial.

   • Message with CRC: $(1101000)$ with remainder $(100)$ gives $(110100100)$

4. Verification: The receiver performs the same division with the appended message $(110100100)$ and checks if the remainder is zero.

   • If the remainder is zero, the data is correct. Otherwise, there was an error during transmission.

Summary

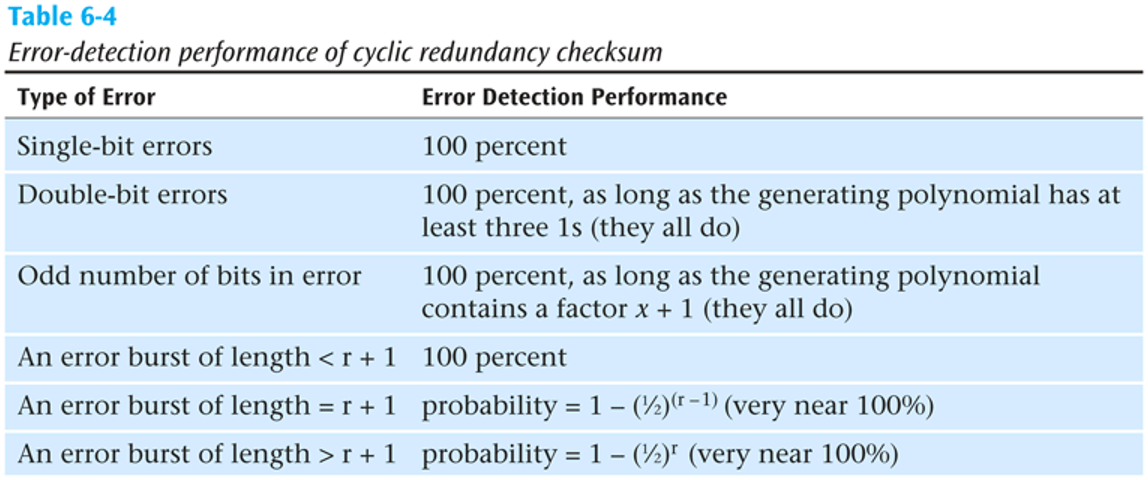
Error detection performance

• CRC: Utilizes polynomial arithmetic for error detection.
• Process: Involves polynomial division and appending the remainder.
• Example: For data $(1101)$ and generator polynomial $(x^3+x+1)$, the remainder after division is $(100)$.